Euler-Lagrange Equation

1. 개념 정리 [1]

아래와 같은 적분식 $I$를 최소로 만드는 $y(x)$를 찾아야하는 문제가 있다.

\[\begin{equation} I = \int _ { x _ { 1 } } ^ { x _ { 2 } } \sqrt { 1 + y ^ { \prime 2 } } d x \end{equation}\]

$y(x)$가 정해져 있는 경우에는 $\frac{dI}{dx} = 0$을 찾으면 되지만 여기서는 $y(x)$가 정해져 있지 않으므로 $y(x)$도 독립변수가 되어 $x$에 대한 미분으로 값을 $I$의 최소값을 찾을 수가 없다.

이 문제를 해결하기 위해서 $y(x)$를 extremal(극값)으로 생각하고 임의의 $\epsilon$, $\eta$을 도입하여 새로운 $Y(x)$를 정의한다.

\[Y(x) = y(x) + \epsilon \eta (x)\]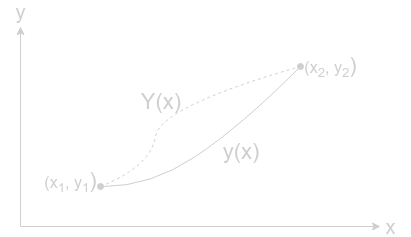
Y(x)
Y(x)
$\eta(x)$
$\eta(x)$

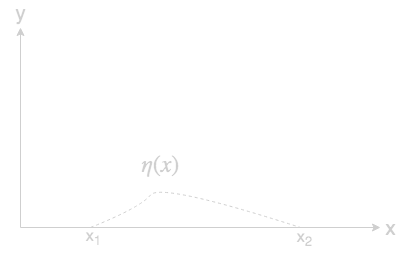
$\eta$는 미분가능하고 $x_1$, $x_2$에서 0인 값을 갖으면서 random인 함수이다. $\eta$와 $\epsilon$의 함수인 $Y(x)$를 이용하면 모든 $I$를 표현 할 수 있으므로 $y(x)$를 해로 가정하고 $Y(x)$의 변화를 이용하여 문제를 풀어간다.

\[I = \int _ { x _ { 1 } } ^ { x _ { 2 } } \sqrt { 1 + Y ^ { \prime 2 } } d x\]

$\epsilon$이 0인 경우 $Y(x)=y(x)$이므로 $I$는 최소값을 가져야한다. 수식으로 표현하면 다음과 같다.

\[\frac { d I } { d \epsilon } = 0 \quad \text { when } \epsilon = 0\]

이제 $x$와 $\epsilon$을 이용하여 문제를 풀어나간다. prime($\prime$)은 x에 대한 미분을 뜻한다.

\[Y ^ { \prime } ( x ) = y ^ { \prime } ( x ) + \epsilon \eta ^ { \prime } ( x ) \Rightarrow \frac { d Y ^ { \prime } } { d \epsilon } = \eta ^ { \prime } ( x )\] \[\frac { d I } { d \epsilon } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \frac { 1 } { 2 } \frac { 1 } { \sqrt { 1 + Y ^ { \prime 2 } } } 2 Y ^ { \prime } \left( \frac { d Y ^ { \prime } } { d \epsilon } \right) d x\]

$\epsilon$이 0인 경우 $Y(x)=y(x)$이므로 위의 수식은 다음과 같다.

\[\left( \frac { d I } { d \epsilon } \right) _ { \epsilon = 0 } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \frac { y ^ { \prime } ( x ) \eta ^ { \prime } ( x ) } { \sqrt { 1 + y ^ { \prime 2 } } } d x = 0\]

변수를 치환하고 부분적분을 수행한다.

\[u = y ^ { \prime } / \sqrt { 1 + y ^ { \prime 2 } } , \quad d v = \eta ^ { \prime } ( x ) d x\] \[\left( \frac { d I } { d \epsilon }\right) _ { \epsilon = 0 } =\left. \frac { y^\prime} {\sqrt {1 + {y^{\prime}}^2}} \eta ( x ) \right| _ { x _ { 1 } } ^ { x _ { 2 } } - \int _ { x _ { 1 } } ^ { x _ { 2 } } \eta ( x ) \frac { d } { d x } \left( \frac { y^\prime} {\sqrt { 1 + {y^{ \prime }}^2}} \right) d x = 0\]

$\eta$는 $x1$, $x2$에서 0이므로 첫째항은 사라진다. $\frac { d I } { d \epsilon } = 0 \quad \text { when } \epsilon = 0$이므로 $\eta$에 관계 없이 두번재 항도 0이여야 한다. 여기서 $\eta$가 0이 될수도 있지만 $\eta$의 정의를 무작위 함수로 가정하였으므로 모든 상황에서 0이 되려면 아래의 수식이 만족되어야 한다.

\[\frac { d } { d x } \left( \frac { y ^ { \prime } } { \sqrt { 1 + y ^ { \prime 2 } } } \right) = 0\]

즉 $I$가 최소가 되려면 $y^{\prime} = \text{const}$이여야 하고 $y$는 직선이여야 한다.


2. 일반식 유도 [1]

\[I = \int _ { x _ { 1 } } ^ { x _ { 2 } } F ( x , y , y ^ { \prime } ) d x\]

functional $F$가 주어지고 $I$를 최소 혹은 최대로 만드는 $y(x)$를 찾아야 한다.

\[Y ( x ) = y ( x ) + \epsilon \eta ( x )\] \[I ( \epsilon ) = \int _ { x _ { 1 } } ^ { x _ { 2 } } F ( x , Y , Y ^ { \prime } ) d x\] \[\frac { d I } { d \epsilon } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \left( \frac { \partial F } { \partial Y } \frac { d Y } { d \epsilon } + \frac { \partial F } { \partial Y ^ { \prime } } \frac { d Y ^ { \prime } } { d \epsilon } \right) d x\]

${dY}/{d\epsilon}=\eta(x)$이므로

\[\frac { d I } { d \epsilon } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \left[ \frac { \partial F } { \partial Y } \eta ( x ) + \frac { \partial F } { \partial Y ^ { \prime } } \eta ^ { \prime } ( x ) \right] d x\]

$I$가 최대 혹은 최소가 되려면 $dI/d\epsilon = 0$ at $\epsilon = 0$이고 $\epsilon=0$은 $Y=y$를 의미하므로

\[\left( \frac { d I } { d \epsilon } \right) _ { \epsilon = 0 } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \left[ \frac { \partial F } { \partial y } \eta ( x ) + \frac { \partial F } { \partial y ^ { \prime } } \eta ^ { \prime } ( x ) \right] d x = 0\]

부분 적분을 적용하고 위의 예제와 동일한 조건을 적용하면 다음과 같다

\[\int _ { x _ { 1 } } ^ { x _ { 2 } } \frac { \partial F } { \partial y ^ { \prime } } \eta ^ { \prime } ( x ) d x = \left. \frac { \partial F } { \partial y ^ { \prime } } \eta ( x ) \right| _ { x _ { 1 } } ^ { x _ { 2 } } - \int _ { x _ { 1 } } ^ { x _ { 2 } } \frac { d } { d x } \left( \frac { \partial F } { \partial y ^ { \prime } } \right) \eta ( x ) d x\] \[\Downarrow\] \[\left( \frac { d I } { d \epsilon } \right) _ { \epsilon = 0 } = \int _ { x _ { 1 } } ^ { x _ { 2 } } \left[ \frac { \partial F } { \partial y } - \frac { d } { d x } \frac { \partial F } { \partial y ^ { \prime } } \right] \eta ( x ) d x = 0\]

Euler-Lagrange Equation

\[\frac { d } { d x } \frac { \partial F } { \partial y ^ { \prime } } - \frac { \partial F } { \partial y }= 0\]


3. Sympy를 이용한 예제 풀이

3.1. 평면에서 최단 거리

평면에서 $x_1$, $x_2$를 지나는 거리를 구하는 공식은 다음과 같다.

\[I = \int _ { x _ { 1 } } ^ { x _ { 2 } }\sqrt{dx^{2}+dy^{2}} = \int _ { x _ { 1 } } ^ { x _ { 2 } }\sqrt{1+{y^{\prime}}^2}dx\]

$F=\sqrt{1+{y^{\prime}}^2}$로 놓고 sympy를 이용하여 풀어본다.

from sympy import init_printing, symbols, sqrt, Function, sympify
from sympy.printing import latex
from sympy.calculus import euler_equations
from IPython.display import Latex as print_latex
from IPython.display import display

init_printing()

x = symbols('x')
y = Function('y')(x)
dy = y.diff(x)
F = sqrt(1 + dy**2)

display(print_latex(r'$$F='+latex(F) + r'$$'))

answer_euler = euler_equations(F, y, x)

display(print_latex(
    r'$$\frac { d } { d x } \frac { \partial F } { \partial y ^ { \prime } } - \frac { \partial F } { \partial y }='
    + latex(sympify(answer_euler[0]))
    + r'$$'))
\[F=\sqrt{\left(\frac{d}{d x} y{\left (x \right )}\right)^{2} + 1}\] \[\frac { d } { d x } \frac { \partial F } { \partial y ^ { \prime } } - \frac { \partial F } { \partial y }=- \frac{\frac{d^{2}}{d x^{2}} y{\left (x \right )}}{\sqrt{\left(\frac{d}{d x} y{\left (x \right )}\right)^{2} + 1}} \left(1 - \frac{\left(\frac{d}{d x} y{\left (x \right )}\right)^{2}}{\left(\frac{d}{d x} y{\left (x \right )}\right)^{2} + 1}\right) = 0\]

sympy에서 euler_euqations 함수 호출 시 내부에서 $d/dx$를 수행하여 직관적이지 않은 해가 도출되었다. 편미분만 수행해 본다.

partial_df = F.diff(dy)
display(print_latex(r'$$\frac{d}{dx}\left(' + latex(partial_df) + r'\right)=0$$'))
\[\frac{d}{dx}\left(\frac{\frac{d}{d x} y{\left (x \right )}}{\sqrt{\left(\frac{d}{d x} y{\left (x \right )}\right)^{2} + 1}}\right)=0\]

$y(x)$가 직선이여야 $I$가 최소가 되는 것을 확인 할 수 있다.


3.2. Brachistochrone Problem[2]

중력만 작용하는 경우 두 점 사이를 가장 빠르게 이동하는 경로를 계산한다.

\[\frac{1}{2}mv^2 - mgy = 0 \Rightarrow v=\sqrt{2gy}\] \[I = \int{dt} = \int{\frac{ds}{v}}=\frac{1}{\sqrt{2g}}\int_{x_2}^{x_2}{\frac{\sqrt{1+{y^{\prime}}^2}}{\sqrt{y}}dx}\] 
from sympy import symbols, sqrt, diff, simplify
from sympy.printing import latex
from sympy.calculus import euler_equations
from IPython.display import Latex as print_latex
from IPython.display import display
from sympy.physics.mechanics import mechanics_printing, dynamicsymbols
mechanics_printing()

x = symbols('x',real=True)
g = symbols('g',constant=True)  #accleration due to gravity
y = dynamicsymbols('y')

y 미분을 $\frac{dy}{dx}$가 아닌 $\dot{y}$로 표현하기 위해서 dynamicsymbols을 사용한다. dynamicsymbols은 y(t)로 기본 설정되어 있어서 코드에서 y 미분을 t에 대해서 수행하지만 수식상에서는 x에 대한 미분으로 생각하면 된다.

dy = diff(y)

F = sqrt(1 + dy**2)/sqrt(2 * g * y)
display(F)
\[\frac{\sqrt{2} \sqrt{\dot{y}^{2} + 1}}{2 \sqrt{g y}}\] 
euler_answer = euler_equations(F, y, symbols('t'))[0]
display(simplify(euler_answer))
\[\frac{\sqrt{2} \sqrt{g y} \left(2 y \ddot{y} + \dot{y}^{2} + 1\right)}{4 g \dot{y}^{2} + 1^{\frac{3}{2}} y^{2}} = 0\]

euler_equations의 출력은 직관적으로 이해하기 힘든 결과이다. sympy로 euler-lagrange를 푸는 것은 큰 도움이 되지 않는 것 같다. 이후 풀이는 Link된 웹페이지에 참고하면 된다.


4. 참고자료

[1] Mary L. Boas. (2005). 9. Calculus of Variations. Mathematical Methods in the physical sciences (474)
[2] http://pgautam.com.np/blog/2017/12/23/brachistochrone-problem/