타원을 등간격으로 N 등분하기
타원 호의 길이가 동일하도록 N 등분하려 하였지만 쉽지 않았다. 결국 구글신[1]의 도움을 받아 해결하기는 했지만 이 문제는 직관적으로 해결 가능한 문제가 아니기에 여기에 정리해 둔다.
1. 호의 길이 구하기
타원을 적분하기 위한 많은 방법들이 존재한다[2]. 여기서는 incomplete elliptic integral of the second kind[3]을 이용한다.
\[E\left( \phi ,k \right) \equiv \int _{ 0 }^{ \phi }{ \sqrt { 1-{ k }^{ 2 }\sin ^{ 2 }{ (\theta) } } } d\theta\] \[k=\sqrt{1 - b^2 / a^2}, \quad\quad\quad \text{a: 장축, b: 단축}\]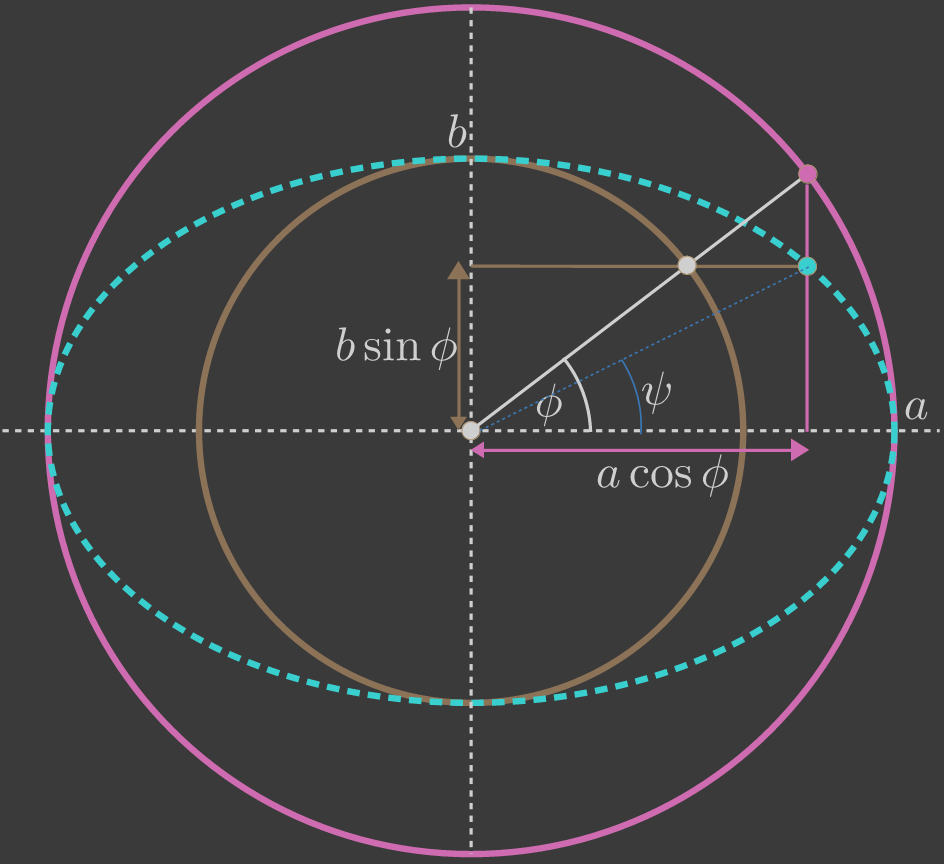
여기서 $\phi$는 원점과 타원 위의 점과의 각도 $\psi$ 와는 다르다. $\phi$는 장축을 반지름으로 하는 원위의 점과 원점과의 각도이다.
위의 함수를 이용하여 타원 둘레($c$)를 구하는 공식은 다음과 같다.
\[c = 4aE\left(\pi/2, k\right)\]즉 incomplete elliptic integral of the second kind 함수를 이용하면 장축 a 단축 b인 타원에서 $\phi$ 각도만큼 이동하였을 경우의 호의 길이를 계산 할 수 있다.
2. Code [4]
Python을 이용하여 타원을 등간격으로 N 등분하는 각도를 계산해 본다. 위에서 소개한 incomplete elliptic integral of the second kind 함수는 scipy에서 쉽게 찾을 수 있다. 이 함수의 결과가 등간격이 되는 입력 $\phi$을 구하는 문제는 scipy의 root함수를 이용하면 쉽게 해결 할 수 있다.
2.1. 함수 선언
from scipy.optimize import root as find_root
from numpy.core.umath import pi
from numpy.core.numeric import arange, ndarray
from scipy.special import ellipeinc
def ang_for_equidistant_in_ellipse(num, r_long, r_short):
"""호의 길이가 등간격이 되도록 타원을 N등분하는 각도를 계산한다.
Parameters
----------
num : int
r_long : float
r_short : float
Returns
-------
angles : ndarray
[rad].
"""
angles = 2 * pi * arange(num) / num # 수치 해석에 사용할 각도 초기값
if r_short != r_long:
e = (1.0 - r_short ** 2.0 / r_long ** 2.0) ** 0.5
perimeter = ellipeinc(2.0 * pi, e)
arcs = arange(num) * (perimeter / num)
res = find_root(lambda x: (ellipeinc(x, e) - arcs), angles)
angles = res.x
return angles
2.2. 예제
a = 20
b = 10
n = 16
phi = ang_for_equidistant_in_ellipse(n, a, b)
e = (1.0 - b ** 2.0 / a** 2.0) ** 0.5
arcs = ellipeinc(phi, e) # Phi 각도별 호의 길이
2.3. 예제 결과 확인
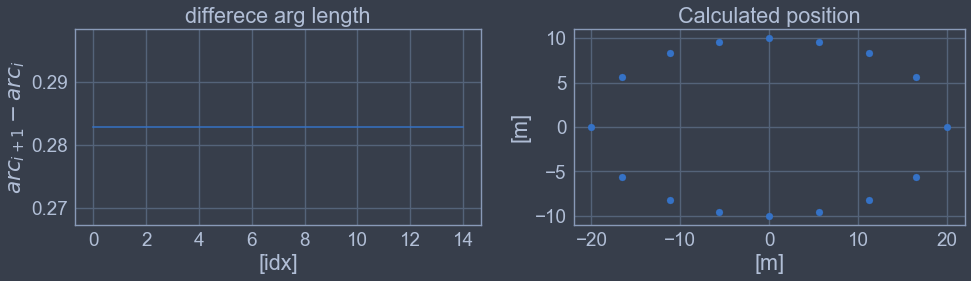
3. 참고 자료
[1] https://math.stackexchange.com/questions/172766/calculating-equidistant-points-around-an-ellipse-arc
[2] https://en.wikipedia.org/wiki/Elliptic_integral
[3] http://mathworld.wolfram.com/EllipticIntegraloftheSecondKind.html
[4] https://stackoverflow.com/questions/6972331/how-can-i-generate-a-set-of-points-evenly-distributed-along-the-perimeter-of-an