빛의 반사 및 굴절의 특성 유도

Fermat의 원리[1]는 ‘빛은 최단 시간으로 이동할 수 있는 경로를 택한다’는 것으로 이 원리를 이용하여 반사 및 굴절의 특성을 유도한다.


1. 빛의 반사 유도

빛의 반사 법칙은 그림 1에서 ${\theta}$(입사각)과 ${\phi}$(반사각)이 항상 같다는 것을 말한다.

빛의 반사
그림 1. 빛의 반사
\[A=\left(x_1, y_1\right)\] \[B=\left(x_2, y_2\right)\] \[P=\left(x, 0\right)\]

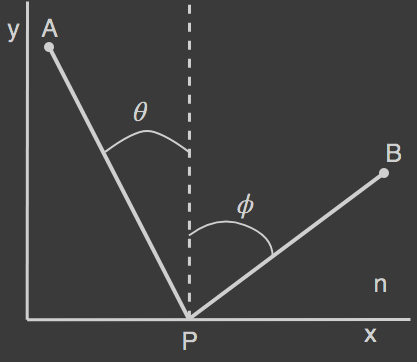
빛은 최단 시간으로 이동할 수 있는 경로를 택한다는 특성[1]을 이용하면 ${\theta}$와 ${\phi}$가 같음을 보일 수 있다.

A, B는 고정위치이고 P를 변하는 위치라고 가정하면 반사되는 빛의 이동경로는 APB가 된다.
빛의 이동거리를 D=$|APB|$로 놓으면 빛의 이동 시간 $T=\left((n/c)D\right)$로 정리 할 수 있다.

최단 시간을 가지는 P를 계산하기 위해서 T의 미분을 이용하여 T가 최소가 되는 x를 계산한다.

\[\frac{dt}{dx} = \left(\frac{n}{c}\frac{dD}{dx}\right)=0\]

이렇게 구한 x로 입사각과 반사각이 동일함을 보인다.


1.1. 빛의 이동 거리(D)

from IPython.display import display
from sympy.printing import latex
from IPython.display import Latex
from sympy import init_printing, symbols, sqrt, diff, solve, Abs, simplify
init_printing()

x = symbols('x', real=True)
x1, x2 = symbols('x_1 x_2', real=True, constant = True)
y1, y2 = symbols('y_1 y_2', positive=True, constant = True)

D = sqrt((x1 - x)**2 + y1**2) + sqrt((x2 - x)**2 + y2**2)
Latex('$$D=' + latex(D) + '$$')
\[D=\sqrt{y_{1}^{2} + \left(- x + x_{1}\right)^{2}} + \sqrt{y_{2}^{2} + \left(- x + x_{2}\right)^{2}}\]


1.2. D의 미분

dD = diff(D, x)
\[\frac{dD}{dx}=\frac{x - x_{1}}{\sqrt{y_{1}^{2} + \left(- x + x_{1}\right)^{2}}} + \frac{x - x_{2}}{\sqrt{y_{2}^{2} + \left(- x + x_{2}\right)^{2}}}\]


1.3. $\frac{dD}{dx}=0$ 으로 하는 x

x_ans= solve(dD, x)
\[x=\left [ \frac{- x_{1} y_{2} + x_{2} y_{1}}{y_{1} - y_{2}}, \quad \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}\right ]\]

첫번째 근은 $y_1$과 $y_2$가 같은 경우 발산하므로 제거한다.

x_ans = x_ans[1]


1.4. $\sin(\theta)$, $\sin(\phi)$

sin_theta = sqrt((x1 - x_ans)**2 + y1**2) / Abs(x1 - x_ans)
sin_phi = sqrt((x2 - x_ans)**2 + y2**2) / Abs(x2 - x_ans)
\[\sin({\theta})=\frac{\sqrt{y_{1}^{2} + \left(x_{1} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}\right)^{2}}}{\left|{x_{1} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}}\right|}\] \[\sin({\phi})=\frac{\sqrt{y_{2}^{2} + \left(x_{2} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}\right)^{2}}}{\left|{x_{2} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}}\right|}\]


1.5. $\sin(\theta)$ / $\sin(\phi)$

display(sin_theta/sin_phi)
\[\frac{\sqrt{y_{1}^{2} + \left(x_{1} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}\right)^{2}} \left|{x_{2} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}}\right|}{\sqrt{y_{2}^{2} + \left(x_{2} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}\right)^{2}} \left|{x_{1} - \frac{x_{1} y_{2} + x_{2} y_{1}}{y_{1} + y_{2}}}\right|}\]

반사각과 입사각이 동일하다면 위의 결과가 1이 나와야 하는데 복잡한 결과가 도출되었다.
이유는 sympy에서 simplify 명령 추가하지 않으면 수식을 정리하지 않기 때문이다.
simplify 이용하여 다시 결과를 뽑아보면 다음과 같다.

display(simplify(sin_theta/sin_phi))
\[1\]

$\frac{\sin(\theta)}{\sin(\phi)} = 1$이므로 반사각과 입사각은 동일하다.


2. 빛의 굴절 유도

빛의 굴절
그림 2. 빛의 굴절

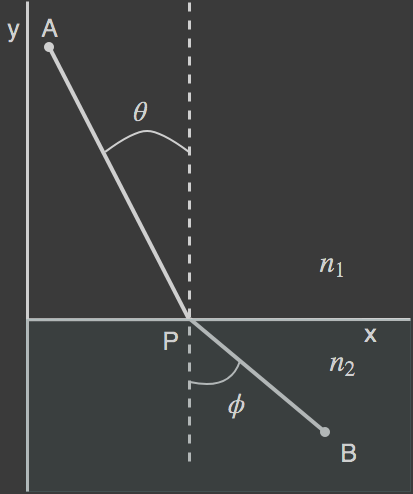
빛의 굴절은 다음과 같은 특성을 가진다.

\[n_1\sin\left(\theta\right) = n_2\sin\left(\phi\right)\]

빛의 굴절도 페르마의 정리를 이용하여 빛의 반사와 유사하게 유도한다.
빛이 A에서 B까지 이동하는데 걸리는 시간 T는 아래와 같이 정리 된다.

\[T = \frac{n_1}{c}|AP| + \frac{n_2}{c}|PB|\]

$\frac{dT}{dx} = 0$에서 위의 수식을 확인한다.


빛의 이동 시간

x = symbols('x', real=True)
x1, x2, y1, y2 = symbols('x_1 x_2 y_1 y_2', real=True, constant = True)
n1, n2, c = symbols('n_1 n_2 c', positive=True, constant = True)

T = (n1/c) * sqrt((x1 - x)**2 + y1**2) + (n2/c) * sqrt((x2 - x)**2 + y2**2)
Latex('$$T=' + latex(T) + '$$')
\[T=\frac{n_{1} \sqrt{y_{1}^{2} + \left(- x + x_{1}\right)^{2}}}{c} + \frac{n_{2} \sqrt{y_{2}^{2} + \left(- x + x_{2}\right)^{2}}}{c}\]


2.1. T의 미분

dT = diff(T, x)
\[\frac{dT}{dx}=\frac{n_{1} \left(x - x_{1}\right)}{c \sqrt{y_{1}^{2} + \left(- x + x_{1}\right)^{2}}} + \frac{n_{2} \left(x - x_{2}\right)}{c \sqrt{y_{2}^{2} + \left(- x + x_{2}\right)^{2}}}=0\]

위의 수식은 빛의 굴절 공식과 동일하다.


3. 참고자료

[1] https://ko.wikipedia.org/wiki/%ED%8E%98%EB%A5%B4%EB%A7%88%EC%9D%98_%EC%9B%90%EB%A6%AC