• 등속 원운동의 구심력 유도
  • 1. 좌표정의
  • 2. Polar 좌표계의 기저 벡터의 미분
  • 3. 각속도 계산
  • 4. 등속 원운동의 가속도 계산
  • 5. 참고자료

등속 원운동의 구심력 유도

등속 원운동의 경우 속력은 일정하나 속도의 방향은 항상 변하기 때문에 가속도 운동이다. 이 가속도의 방향과 크기를 유도한다.

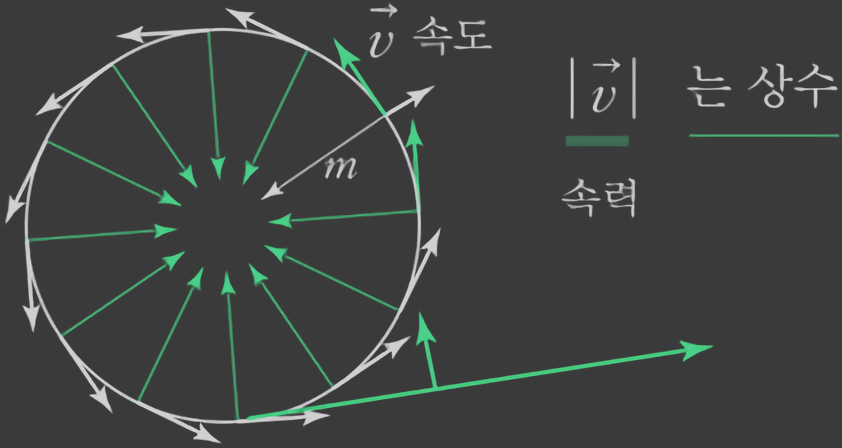
1. 좌표정의

원운동의 중점을 원점으로 설정하고, 원운동하는 물체의 위치 벡터를 $\vec{p}$로 설정한다.

\[\vec{p} = \left( x, y \right)= x \hat{x} + y \hat{y} = \cos{\theta}\hat{x} + \sin{\theta}\hat{y}=\hat{r}\]

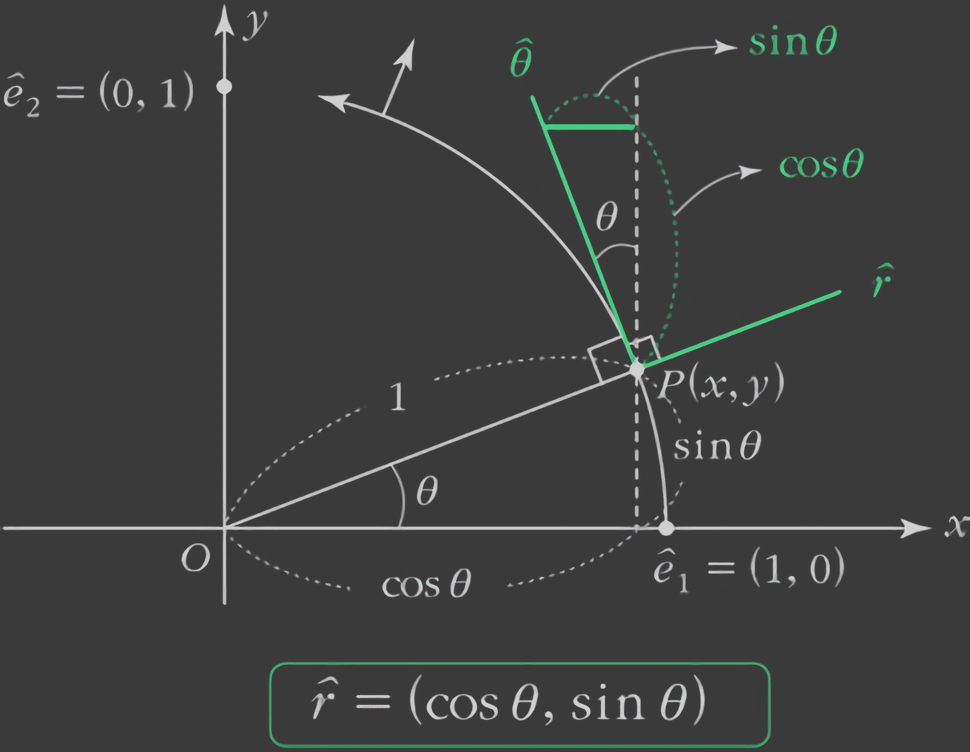
$\vec{p}$는 Polar 좌표계의 $\vec{r}$로 정의 할 수 있고 $\hat{\theta}$은 원주를 돌아가는 접선 방향이므로 $\vec{r}$와 수직이여야 한다.
위의 그림에서 알 수 있듯이 Polar 좌표계의 $\hat{\theta}$은 다음과 같이 정의된다.

\[\hat{\theta} = -\sin{\theta}\hat{x} + \cos{\theta}\hat{y}\]

2. Polar 좌표계의 기저 벡터의 미분

$\hat{r}$, $\hat{\theta}$의 시간변화량을 계산하면 다음과 같다.

\[\left.\begin{array}{l}{ \frac { d \hat { r } } { d t } = \left( \frac { d } { d t } \operatorname { cos } \theta , \frac { d } { d t } \operatorname { sin } \theta \right) = \left( \left( \frac { d } { d \theta } \operatorname { cos } \theta \right) \cdot \frac { d \theta } { d t } , \left( \frac { d } { d \theta } \operatorname { sin } \theta \right) \cdot \frac { d \theta } { d t } \right) }\\{ = \left( - \operatorname { sin } \theta \cdot \dot { \theta } , \operatorname { cos } \theta \cdot \dot { \theta } \right) }\\{ = \dot { \theta } \left( - \operatorname { sin } \theta , \operatorname { cos } \theta \right) = \dot { \theta } \hat { \theta } }\\{ \frac { d \hat { \theta } } { d t } = \left( - \operatorname { cos } \theta \cdot \dot { \theta } , - \operatorname { sin } \theta \cdot \dot { \theta } \right) = - \dot { \theta } \left( \operatorname { cos } \theta , \operatorname { sin } \theta \right) = - \dot { \theta } \hat { r } }\end{array} \right.\]

다시 정리하면 다음과 같다.

\[\frac { d } { d t } \hat { r } = \dot { \hat { r } } = \dot { \theta } \hat { \theta } , \quad \frac { d } { d t } \hat { \theta } = \dot { \hat { \theta } } = - \dot { \theta } \hat { r }\]

3. 각속도 계산

$\dot{\theta}=\frac{d}{dt}\theta$ 는 시간에 대한 각도의 변화로서, 흔히 ‘각속도’(angular velocity)라고 부른다. 각속도는 초당 얼마의 각도만큼 회전했는가를 나타낸다. 각속도의 단위는 sec^-1이다. 각도는 단위가 없는 양이라고 했다. 단위가 없는 각도를 시간으로 미분했으니 단위가 시간의 (^-1)승이 된 것이다. sec^-1 은 특별히 Hz(헤르츠)라고도 부른다. Hz는 진동수 즉, 초당 몇 번 진동하는가를 나타내기도 한다.
각도는 호도법으로 쟀을 때 호의 길이에 대한 반지름의 비율이다. 따라서 호의 길이를 $\ell$ 이라 하면 각속도는 다음과 같다.

\[\dot { \theta } = \frac { d } { d t } \theta = \frac { d } { d t } ( \frac { \ell } { r } ) = \frac { 1 } { r } \frac { d } { d t } \ell = \frac { v } { r }\]

4. 등속 원운동의 가속도 계산

등속 원운동은 속도가 상수인 운동, 즉 $\frac{d}{dt}v=0$인 운동이므로 등속 원운동의 가속도는 아래와 같이 정리 된다.

\[\vec { a } = \frac { d } { d t } \vec { v } = \frac { d } { d t } \left( \nu \hat { \theta } \right)= \frac { d } { d t }v \cdot \hat { \theta } +v\cdot \frac { d } { d t }\hat{\theta}= v \dot { \hat { \theta } } = - v \dot { \theta } \hat { r }\]

위에서 정리한 기적벡터의 각속도를 대입하여 등속 원운동의 가속도를 구한다.

\[\vec { a } = - v \dot { \theta } \hat { r } = - \frac { v ^ { 2 } } { r } \hat { r }\]

5. 참고자료

[1] 이종필. (2017). 18. 고전역학 강의, 이종필의 아주 특별한 상대성이론 강의 (쪽). 동아시아