정사각형 내 임의의 두점의 거리

정사각형 내 임의의 두 점 P1, P2 사이의 거리 기댓값을 계산한다.
P1 = ($x_1$, $y_1$)
P2 = ($x_2$, $y_2$)
$x_1, y_1, x_2, y_2$는 0~1 사이의 uniform random variable로 가정한다.

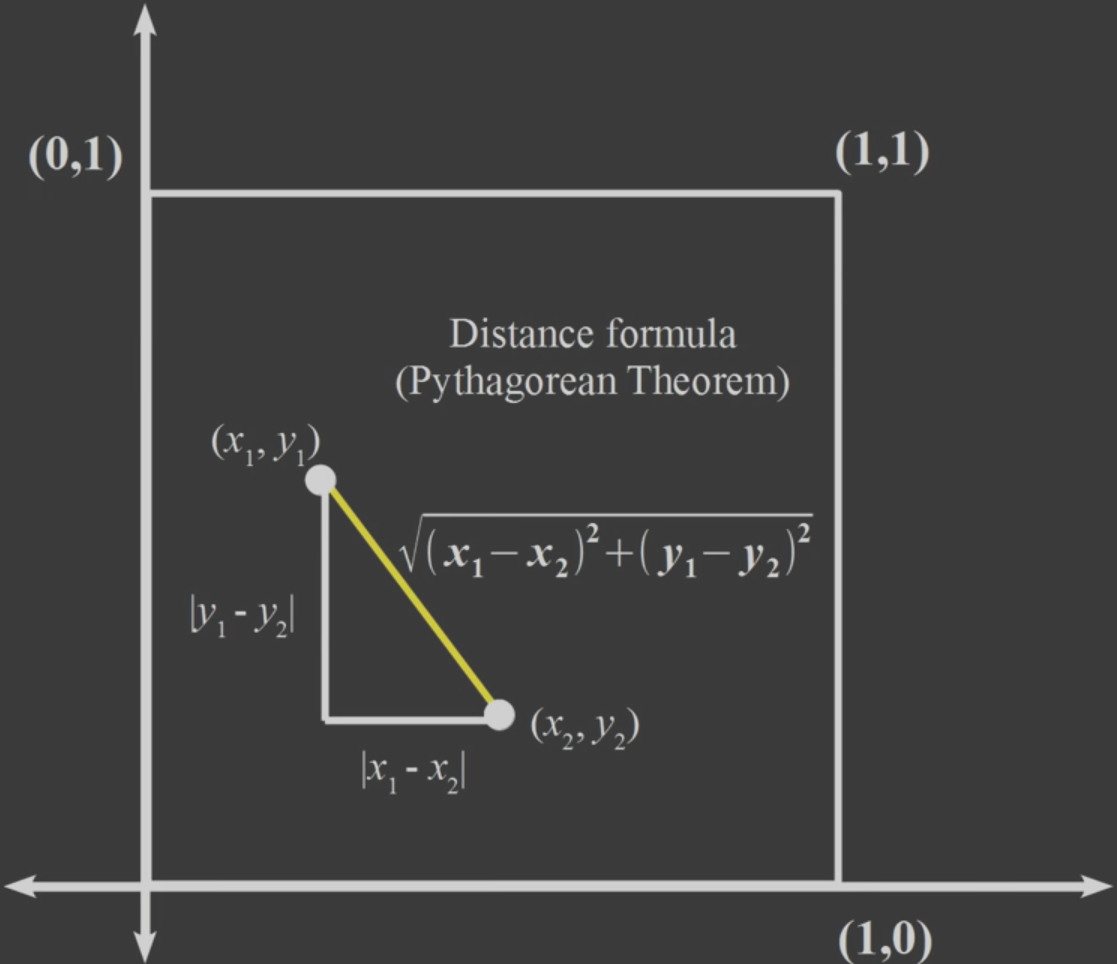
distance img

간단해 보이는 문제이지만 쉽게 풀리지도 않고 답 또한 딱 떨어지지 않는다.


1. Simulation

uniform random 좌표를 생성하여 좌표 간 거리의 평균을 계산한다.

from numpy import sqrt, mean
from numpy.random_intel import uniform

n = 2 ** 26
x1 = uniform(0, 1, n)
x2 = uniform(0, 1, n)
y1 = uniform(0, 1, n)
y2 = uniform(0, 1, n)

distances = sqrt((x1 - x2)**2 + (y1 - y2)**2)
distances_mean = mean(distances)

정사각형 내 두 점 사이의 거리 평균 = 0.5213815545906049


2. 수치해석

거리를 구하는 적분식 근을 scipy의 nquad를 이용하여 구한다.

\[\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ 1 }{ \int _{ 0 }^{ 1 }{ \int _{ 0 }^{ 1 }{ \sqrt { \left( { x }_{ 1 }-{ x }_{ 2 } \right)^2 +\left( { y }_{ 1 }-y_{ 2 } \right)^2 } d{ x }_{ 1 } } d{ x }_{ 2 } } dy_{ 1 } } d{ y }_{ 2 } }\] 
from numpy import sqrt
from scipy.integrate import nquad

integrand = lambda x1, x2, y1, y2: sqrt((x1-x2)**2 + (y1-y2)**2)
(distances_mean, abserr, out_dict) = nquad(integrand, [[0, 1], [0, 1], [0, 1], [0, 1]], full_output=True)

정사각형 내 두 점 사이의 거리 평균 = 0.5214054334862938


3. 함수 적분[1]

위의 수식에서 $|x_1-x_2|=u,\text{ }|y_1-y_2|=v$로 치환한다.
$|a-b|=c$이고 a, b가 uniform random variable이면 c의 PDF는 2(1-c)임을 이용하여 적분식을 정리하면 아래와 같다. [아래 절 참조]

\[4\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ 1 }{ \sqrt { { u }^{ 2 }+{ v }^{ 2 } } \left( 1-u \right) \left( 1-v \right) du } dv }\]



위의 수식을 적분하기 위해 변수를 Polar Form으로 변환한다. 변환 시 적분 구간에 유의 해야한다.

\[\begin{matrix} u=r\cos{\theta} & 0\le{\theta}\le\pi/4 \\ v=r\sin{\theta} & 0\le{r}\le{1/\cos{\theta}} \end{matrix}\]



정사각형 내의 점들의 길이를 구하는 것이므로 r은 $1/\cos{\theta}$를 넘을 수 없다.

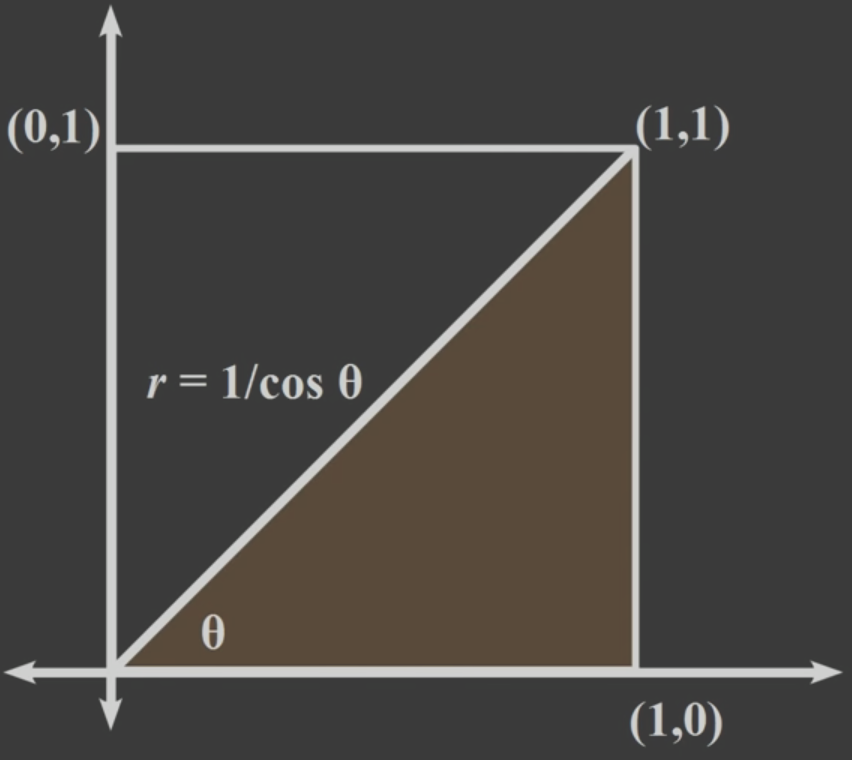
Integral Region



변수를 치환하면 아래와 같고 적분 구간을 정사각형의 절반만 정의하였으므로 2가 곱해진다.

\[4\int _{ 0 }^{ \pi /4 }{ 2\int _{ 0 }^{ 1/\cos { \theta } }{ \sqrt { r^{ { 2 } }{ \cos }^{ { 2 } }\theta +r^{ { 2 } }{ \sin }^{ { 2 } }\theta } (1-r{ \cos }\theta )(1-r{ \sin }\theta )rdr } d\theta }\] \[=8\int _{ 0 }^{ \pi /4 }{ \int _{ 0 }^{ 1/\cos { \theta } }{ r^{ { 2 } }-r^{ { 3 } }{ \cos }\theta -r^{ { 3 } }{ \sin }\theta +r^{ { 4 } }{ \cos }\theta { \sin }\theta dr} d\theta }\] \[=8\int _{ 0 }^{ \pi /4 }{ \frac { { \sec } ^ { 3 } \theta } { 12 } - \frac { { \sec } ^ { 3 } \theta { \tan } \theta } { 20 }d\theta }\] \[=8\cdot \left( \frac { { \sec }\theta { \tan }\theta +{ \ln { \left| { \sec }\theta +{ \tan }\theta \right|}}}{ 24 } -\frac { { \sec }^{ { 3 } }\theta }{ 60 } \right) _{ { 0 } }^{ { \pi /4 } }\] \[=\frac { 2+\sqrt { 2 } +5{ \ln { (\sqrt { 2 } +1) } } }{ 15 }\] \[=0.5214054331647207\]


3.1. |a-b| 의 PDF (Probability Density Function)

두 random variable의 합의 PDF는 각각의 PDF의 Convolution이다

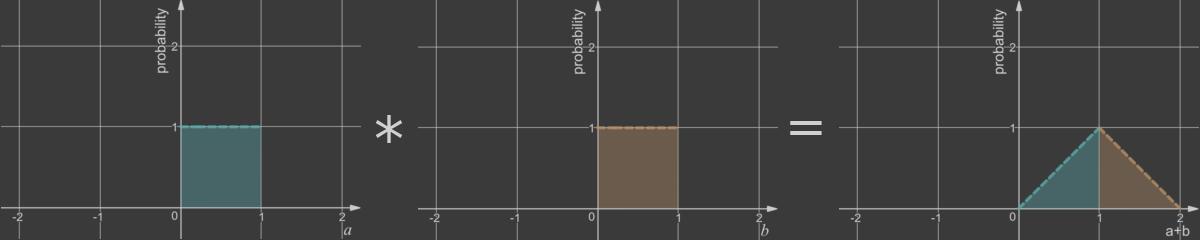
a plus b pdf



a-b의 pdf는 c=-b이고 a+c의 pdf와 동일 하므로 PDF(a) * PDF(-b)로 계산된다.

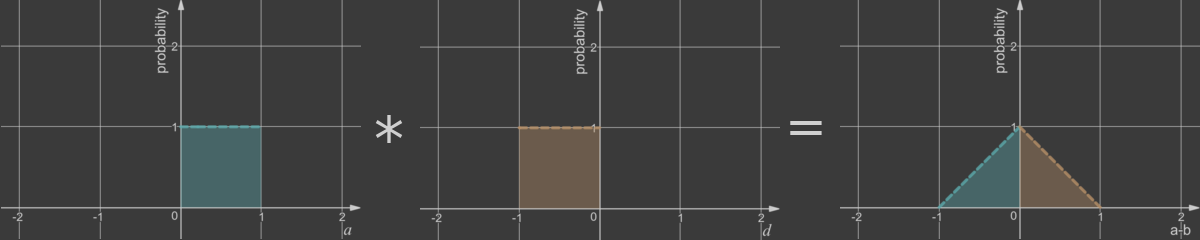
a minus b pdf



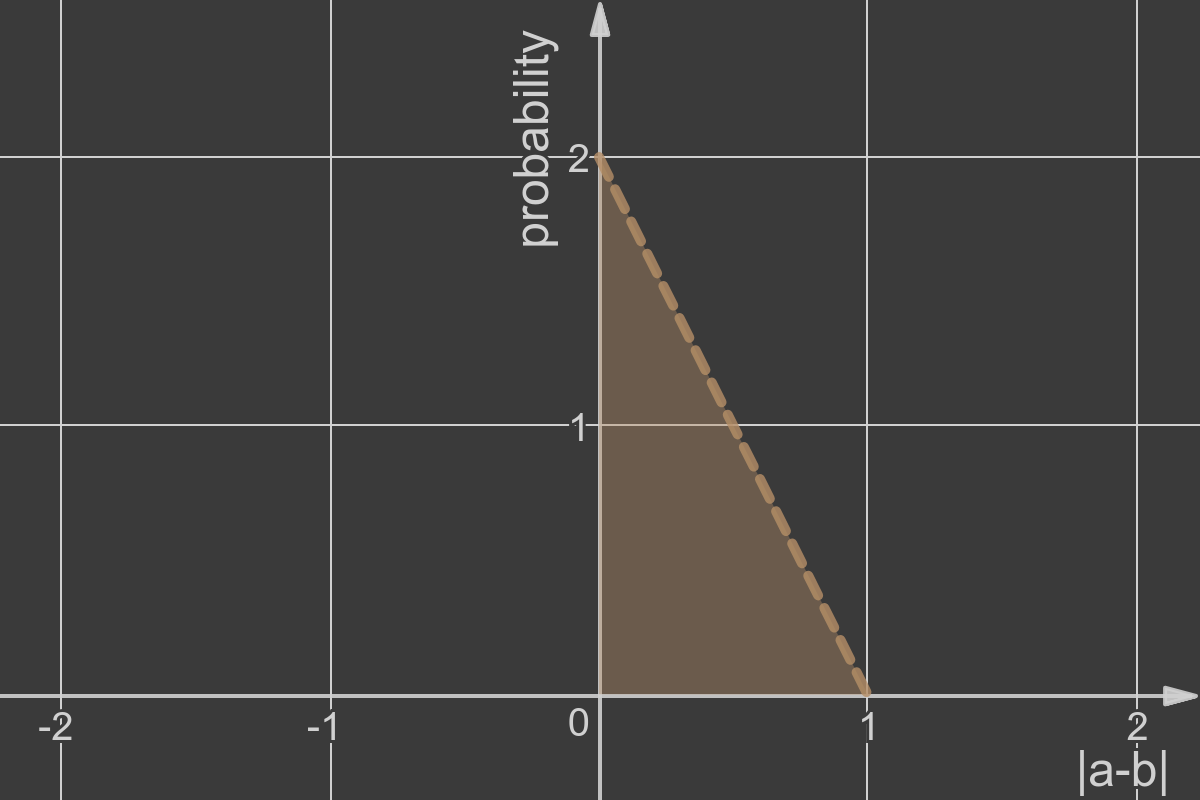
(a-b) < 0인 경우와 (a-b) > 0인 경우의 확률은 대칭이므로 |a-b|의 확률은 아래와 같다.

|a-b| pdf


4. 참고자료

[1] https://www.youtube.com/watch?v=i4VqXRRXi68&t=275s