Principle of Stationary Phase(POSP)

넓은 주파수 대역을 가지는 1-D 함수의 Fourier Transform 근사 방법이다. Super Chirp( $e^{\pm i \pi t^n}$ ) 형태의 Close form이 없는 함수의 주파수 특성을 유도하기에 매우 유용하다.

I (f) = \int_{- \infty}^{+ \infty} r (t) e^{i f \cdot μ (t)} d t

$I ( f ) = \int _ { - \infty } ^ { + \infty } r ( t ) e ^ { i f \cdot \mu ( t ) } d t$

r (t), μ (t) = real-valued function

$r ( t ), \mu ( t ) \text{= real-valued function}$

위의 적분식에서 지수 함수 $e ^ { i f \cdot \mu ( t ) }$ 의 진동의 속도는 $f$ 와 $\mu ( t )$ 에 비례할 것이다. 만약 f가 크다면, ${\mu} ^{\prime} ( t ) = 0$ 을 제외한 영역에서 $e ^ { i f \cdot \mu ( t ) }$ 는 -1과 1 매우 빠르게 진동할 것이고 $r ( t )$ 보다 빠르게 진동한다면 지수 함수의 큰 진동 때문에 값들이 상쇄되어 적분 결과는 매우 작을 것이다.
${\mu}^{\prime} ( t_0 ) = 0$ 인 영역의 $t_0$ 을 Stationary point라고 부르고 $t_0$ 의 영역을 적분 값으로 근사화하는 것을 Principle of Stationary Phase라고 한다.

1. Principle of Stationary Phase를 이용한 Fourier Transform 근사

함수 $x(t)$ 의 Fourier Transform은 아래와 같다.

\begin{matrix} X (f) = F_{1} {x (t)} = \int_{- \infty}^{+ \infty} x (t) e^{- 2 π i f t} d t = \int_{- \infty}^{+ \infty} (| x (t) | e^{i Φ {x (t)}}) e^{- 2 π i f t} d t = \int_{- \infty}^{+ \infty} | x (t) | e^{i (Φ {x (t)} - 2 π f t)} d t \end{matrix}

$\left.\begin{array}{l}{ X ( f ) = F _ { 1} \{ x ( t ) \} = \int _ { - \infty } ^ { + \infty } x ( t ) e ^ { - 2\pi i f t } d t }\\{ = \int _ { - \infty } ^ { + \infty } ( | x ( t ) | e ^ { i \Phi \{ x ( t ) \} } ) e ^ { - 2\pi i f t } d t }\\{ = \int _ { - \infty } ^ { + \infty } | x ( t ) | e ^ { i ( \Phi \{ x ( t ) \} - 2\pi f t ) } d t }\end{array} \right.$

$\mu ( t )$ 를 아래와 같이 정의한다.

μ (t) = \frac{1}{f} Φ {x (t)} - 2 π t

$\mu ( t ) = \frac { 1} { f } \Phi \{ x ( t ) \} - 2\pi t$

$\mu ( t )$ 로 치환한다. 여기서 $f$ 는 매개변수이고 피적분함수와 독립이므로 $\mu ( t )$ 에 포함되어 있어도 관계 없다.

X (f) = \int_{- \infty}^{+ \infty} | x (t) | e^{i f \cdot μ (t)} d t

$X ( f ) = \int _ { - \infty } ^ { + \infty } | x ( t ) | e ^ { i f \cdot \mu ( t ) } d t$

$\mu ( t )$ 를 Taylor series 전개한다.

\begin{matrix} μ (t) = μ (t_{0}) + (t - t_{0}) μ^{'} (t_{0}) + \frac{(t - t_{0})^{2}}{2} μ^{''} (t_{0}) + \dots + \frac{(t - t_{0})^{n}}{n!} μ^{(n)} (t_{0}) + \dots \end{matrix}

$\left.\begin{array} { c } { \mu(t) = \mu ( t _ { 0} ) + ( t - t _ { 0} ) \mu ^ { \prime } ( t _ { 0} ) + \frac { ( t - t _ { 0} ) ^ { 2} } { 2} \mu ^ { \prime \prime } ( t _ { 0} ) } \\ { + \cdots + \frac { ( t - t _ { 0} ) ^ { n } } { n ! } \mu ^ { ( n ) } ( t _ { 0} ) + \cdots } \end{array} \right.$

$\mu ^{\prime} { ( t_0 ) } = 0$ 이 되는 stationary point $t_0$ 를 잡아서 위의 Fourier Transform 수식에 대입한다.

\begin{matrix} X (f) = \int_{- \infty}^{+ \infty} | x (t) | exp [+ i f (μ (t_{0}) + μ^{''} (t_{0}) \frac{(t - t_{0})^{2}}{2} + \dots)] d t \end{matrix}

$\left.\begin{array} { q }{ X ( f ) = \int _ { - \infty } ^ { + \infty } | x ( t ) | \operatorname{exp} [ + i f ( \mu ( t _ { 0} ) + \mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} + \cdots ) ] d t}\end{array} \right.$

= \int_{- \infty}^{+ \infty} | x (t) | (exp [+ i f \cdot μ (t_{0})] \cdot exp [+ i f (μ^{''} (t_{0}) \frac{(t - t_{0})^{2}}{2})] \dots) d t

$= \int _ { - \infty } ^ { + \infty } | x ( t ) | ( \operatorname{exp} [ + i f \cdot \mu ( t _ { 0} ) ] \cdot \operatorname{exp} [ + i f (\mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} )]\dots ) d t$

$= \operatorname{exp} [ + i f \cdot \mu ( t _ { 0} ) ] \int _ { - \infty } ^ { + \infty } | x [ t ] | \prod _ { n = 2} ^ { + \infty } ( \operatorname{exp} [ + i f ( \mu ^ { ( n ) } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { n} } { n!} ) ] ) d t$

f가 크다면 지수함수의 진동이 $| x ( t ) |$ 의 변화량 보다 매우 크다고 가정할 수 있고 이 경우 적분 전체에 미치는 영향을 미미할 것으로 간주한다.
이런 가정하에 적분값을 stationary point 주변값으로 근사화 시킬 수 있다. 또한 n > 2일 경우 $t_0$ 부근에서 $(t - t_0)^n « (t - t_0)^2$ 이므로 위의 수식은 아래와 같이 근사화 된다.
이 근사화로 $|x ( t )|$ 를 $|x ( t _ { 0} )|$ 로 치환 할 수 있다.

$\hat { X } [ | f | > > 0] \cong | x ( t _ { 0} ) | \operatorname{exp} [ + i f \cdot \mu ( t _ { 0} ) ] \int _ { t _ { 0} - \epsilon } ^ { t _ { 0} + \epsilon } \operatorname{exp} [ + i f \cdot \mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} ] d t$

적분 Term을 계산하기 위해 한번 더 근사화가 필요하다. Quadratic-phase를 적분할 경우에도 stationary point에 대부분의 값이 집중되어 있으므로 아래와 같이 근사화 시킨다.

$\int _ { t _ { 0} - \epsilon } ^ { t _ { 0} + \epsilon } \operatorname{exp} [ + i f \cdot \mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} ] d t \cong \int _ { - \infty } ^ { + \infty } \operatorname{exp} [ + i f ( \mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} ) ] dt$

$\pi u^2 \equiv \frac { 1} { 2} f \mu ^ { \prime \prime } ( t _ { 0} ) ( t - t _ { 0} ) ^ { 2}$ 을 이용해 위의 근사식을 변수 치환한다.

$\int _ { t = - \infty } ^ { t = + \infty } \operatorname{exp} [ + i f ( \mu ^ { \prime \prime } ( t _ { 0} ) \frac { ( t - t _ { 0} ) ^ { 2} } { 2} ) ] d t = ( \sqrt { \frac { 2\pi } { f \mu ^ { \prime \prime } ( t_ { 0} ) } } ) \int _ { u = - \infty } ^ { u = + \infty } \operatorname{exp} [ + i \pi u ^ { 2} ] d u$

치환된 수식은 central ordinate theorem을 적용하여 계산할 수 있다.

$( \sqrt { \frac { 2\pi } { f \mu ^ { \prime \prime } ( t _ { 0} ) } } ) \int _ { u = - \infty } ^ { u = + \infty } \operatorname{exp} [ + i \pi u ^ { 2} ] d u = ( \sqrt { \frac { 2\pi } { f \cdot \mu ^ { \prime \prime } ( t _ { 0} ) } } ) \quad \operatorname{exp} [ + i \frac { \pi } { 4} ]$

위의 수식을 정리하면 stationary point $t_0$ 를 가지는 함수에 대한 Fourier Transform 근사식은 다음과 같다.

$\hat { X } ( | f | > > 0) \cong | x ( t _ { 0} ) | ( \sqrt { \frac { 2\pi } { f \cdot \mu ^ { \prime \prime } ( t _ { 0} ) } } ) \quad \operatorname{exp} [ + i \frac { \pi } { 4} ] \quad \operatorname{exp} [ + i f \cdot \mu ( t _ { 0} )]$

만약 stationary point가 여러개일 경우 staionary point별로 계산 후 합한다.

2. Linear Frequency Modulation 신호에 POSP 적용

시간에 따라 주파수가 선형적으로 변화하는 Linear Frequency Modulation 신호를 Chirp이라고 부른다.

$\text{chirp}=e^{i \pi k_r t^2}$

$k_r \text{: Chirp rate}$

Chirp의 경우 2차항만 존재하므로 Taylor Series에 의한 오차가 없어서 POSP를 이용한 근사가 매우 정확하다.

Chirp의 경우 $\mu$ 는 아래와 같이 정의 되고

$\mu(t) = \frac{\pi k_r t^2}{f} - 2 \pi t$

위의 POSP 최종 공식에 넣으면 아래와 같다.

$X(f) = \frac{1}{\sqrt{k_r}} e ^{-i \pi (\frac{f^2}{k_r} + \frac{1}{4})}$

3. Sympy를 이용한 Chirp의 Fourier Transform

Sympy를 이용하여 Chirp의 적분 결과를 확인한다. Sympy를 사용하면 계산 결과 검토 및 복잡한 연산의 힌트를 찾는데 도움이 된다.

from sympy import Symbol, pi, exp
from sympy.integrals.transforms import fourier_transform

sym_t = Symbol('t', real=True)
sym_f = Symbol('f', real=True)
sym_k_r = Symbol('k_r', positive=True)

chirp = exp(-1j * pi * sym_k_r * sym_t**2)
chirp_fourier_sympy = fourier_transform(chirp, sym_t, sym_f)

$\text{chirp: }e^{- 1.0 i \pi k_{r} t^{2}}$

$\text{chirp fourier by sympy: }\frac{1.0 i e^{i \pi \left(\frac{f^{2}}{k_{r}} - \frac{3}{4}\right)}}{\sqrt{k_{r}}}$

위의 POSP 수식과 Sympy의 Fourier Transform 결과가 동일한 것을 알 수 있다

4. Discrete Time Fourier Series(DTFS)와 POSP 결과 비교

import numpy as np
from numpy import arange, exp, pi
Tp = 40e-6  # [sec]
fs = 50e6  # [Hz]
bw = 20e6  # [Hz]
kr = bw/Tp  # chirp rate
dt = 1/fs

num_sample = int(Tp*fs)

t = (arange(num_sample) - num_sample/2) * dt

chirp_discrete_time = exp(1j * pi * kr * t**2)

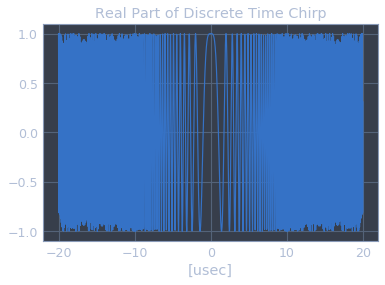
from sympy import lambdify
from numpy.fft import fftshift, fft

frequency = (arange(num_sample) - num_sample/2) / num_sample * fs
chirp_fourier_series = fftshift(fft(chirp_discrete_time))

chirp_fourier_sympy_subs = lambdify( sym_f, chirp_fourier_sympy.subs(sym_k_r, kr), "numpy" )
chirp_fourier_posp = chirp_fourier_sympy_subs(frequency)

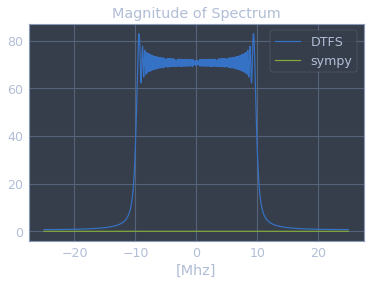
sympy 결과와 DTFS의 결과가 전혀 다르게 나타난다. 그 이유는 FFT의 특성과 Fourier transform의 scaling property 때문이다.

Python에서 생성한 discrete chirp이 $x[n]$ 이고 POSP 유도에서 쓰인 continuous time domain의 chirp이 $x(t)$ 이면 다음과 같은 관계를 갖는다.

$x[n]=x(n \cdot dt)$

하지만 fft의 경우 입력된 신호의 Sampling 간격 dt를 1로 가정하고 주파수 Spectrum을 계산하기 때문에 POSP와 FFT의 결과가 달라지게 되고 그 차이는 Fourier transform의 scaling property를 이용하여 아래와 같이 구할 수 있다.

$|F(x[n \cdot 1])| = \frac{|F(x[n \cdot dt])|}{dt}$

chirp_fourier_posp = chirp_fourier_sympy_subs(frequency)/dt

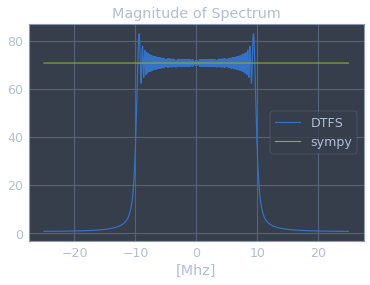
참고자료

https://www.cis.rit.edu/class/simg738/Handouts/stationary_phase.pdf

Principle of Stationary Phase

Principle of Stationary Phase(POSP)

1. Principle of Stationary Phase를 이용한 Fourier Transform 근사

2. Linear Frequency Modulation 신호에 POSP 적용

3. Sympy를 이용한 Chirp의 Fourier Transform

4. Discrete Time Fourier Series(DTFS)와 POSP 결과 비교

참고자료

Recent Posts

Python에서 이진파일 (Binary file) 입출력

타원을 등간격으로 N 등분하기

Computed Tomography (CT) 촬영의 원리

Numba를 이용한 Cuda 프로그램 예제

Tags

cuda (2)

github (1)

jupyter (1)

math (8)

matlab (2)

physics (3)

pycharm (1)

python (14)

signal_system (1)

sympy (4)